[레드 블랙 트리의 노드 삭제]
[삭제]
레드블랙트리의 삭제연산은 기본적으로 이진 탐색 트리의 삭제연산과 같다 .
다만 , 삭제후 레드 블랙 트리의 무너진 규칙을 수습하는 과정이 더해질 뿐이다 .
[ 무너진 규칙의 복구 ]
무너진 규칙의 복구를 위해 레드 블랙 트리의 규칙을 다시 떠올리자면
- 모든 노드는 검정색 아니면 빨간색이다 .
- 루트 노드는 검은색이다 .
- 잎 노드는 검은색이다 .
- 빨간 노드의 자식들은 모두 검은색이다 . 하지만 검은 노드의 자식이 빨간색일 필요는 없다 .
- 루트 노드부터 모든 잎 노드 사이에 있는 검은색 노드의 수는 모두 동일하다 .
노드를 하나 삭제했을때 다음의 경우로 나뉜다 .
01 . 삭제한 노드가 빨간색일때
=>아무것도 처리할 필요가 없다 . 위의 규칙에 위반사항이 없다
02 . 삭제한 노드가 검정색일때
가장먼저 5번 규칙이 무너진다 .
또한 삭제한 노드의 부모와 자식이 빨간색인 경우 4번 규칙도 무너진다 .
=>위의 상황을 한번에 보완하는 방법이 있다 . 삭제한 노드를 대체하는 노드를 검정색으로 칠하는 것이다.
해당 케이스는 대체 노드의 색에따라 다시 나뉜다
02-1 . 대체노드가 빨간색일때
=>검정색으로 칠하여 끝낸다
02-2 . 대체노드가 검정색일때
=>이때는 5번 규칙을 위반한다 .이경우 검정색으로 덧칠한다 .
이렇게 검정색을 2개 가지는 노드를 이중흑색노드라고 한다 .

해당 문제는 이제 1번의 문제로 바뀌었다 . 이중흑색은 검은색,빨간색도 아니기 때문이다 .
(다만 , 이중흑색은 실제로는 5번인 문제의 해결을 쉽게 하기 위해 사용하는 도구일뿐이다) .
해당 경우는 이중흑색 노드의 형제와 조카들의 상태에 따라 다시 4가지로 나뉜다 .
다읨의 경우는 이중흑색 노드가 부모 노드의 왼쪽 자식인 경우에 한한다 . (오른쪽 자식의 경우는 좌/우 바꾸자)
02-2 -A. 형제가 빨간색인경우

=> 형제를 검정색 , 부모를 빨간색으로 칠한다 . 부모를 기준으로 좌회전 한다 .
해당 경우 이중흑색 노드는 남아있지만 , 형제는 검은색 노드로 바뀐다 .
이제 해당 문제는 B,C,D중 하나의 문제로 변하였다 .
02-2 -B. 형제가 검은색 + 형제의 양쪽 자식이 모두 검은색
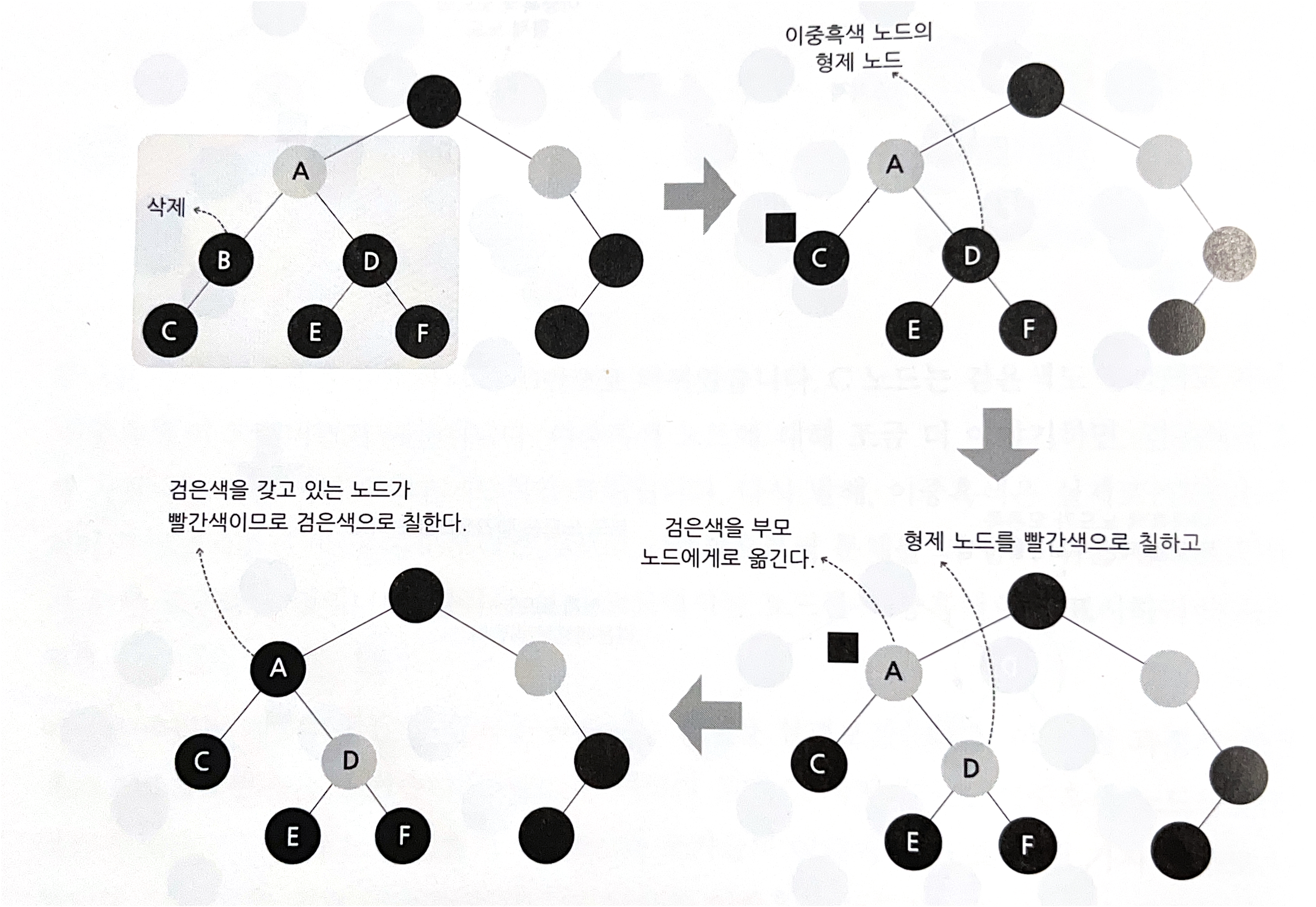
=>형제노드를 빨간색으로 칠하고 , 이중흑색 노드의 검정을 부모에게 넘겨준다 .
부모는 다시 ABCD의 상황에 대처한다 .
02-2 -C. 형제가 검은색 + 형제의 왼쪽 자식은 빨간색 / 오른쪽 자식은 검은색
=>형제를 빨간색으로 칠하고 왼쪽 자식을 검은색으로 칠한 후 형제노드를 기준으로 우회전을 수행한다 .
이중흑색 노드는 여전히 그대로이다 .
이제 해당 문제는 형제가 검은색 오른쪽 자식이 빨간색인 경우로 바뀌었다 .
02-2 -D. 형제가 검은색 + 형제의 오른쪽 자식이 빨간색
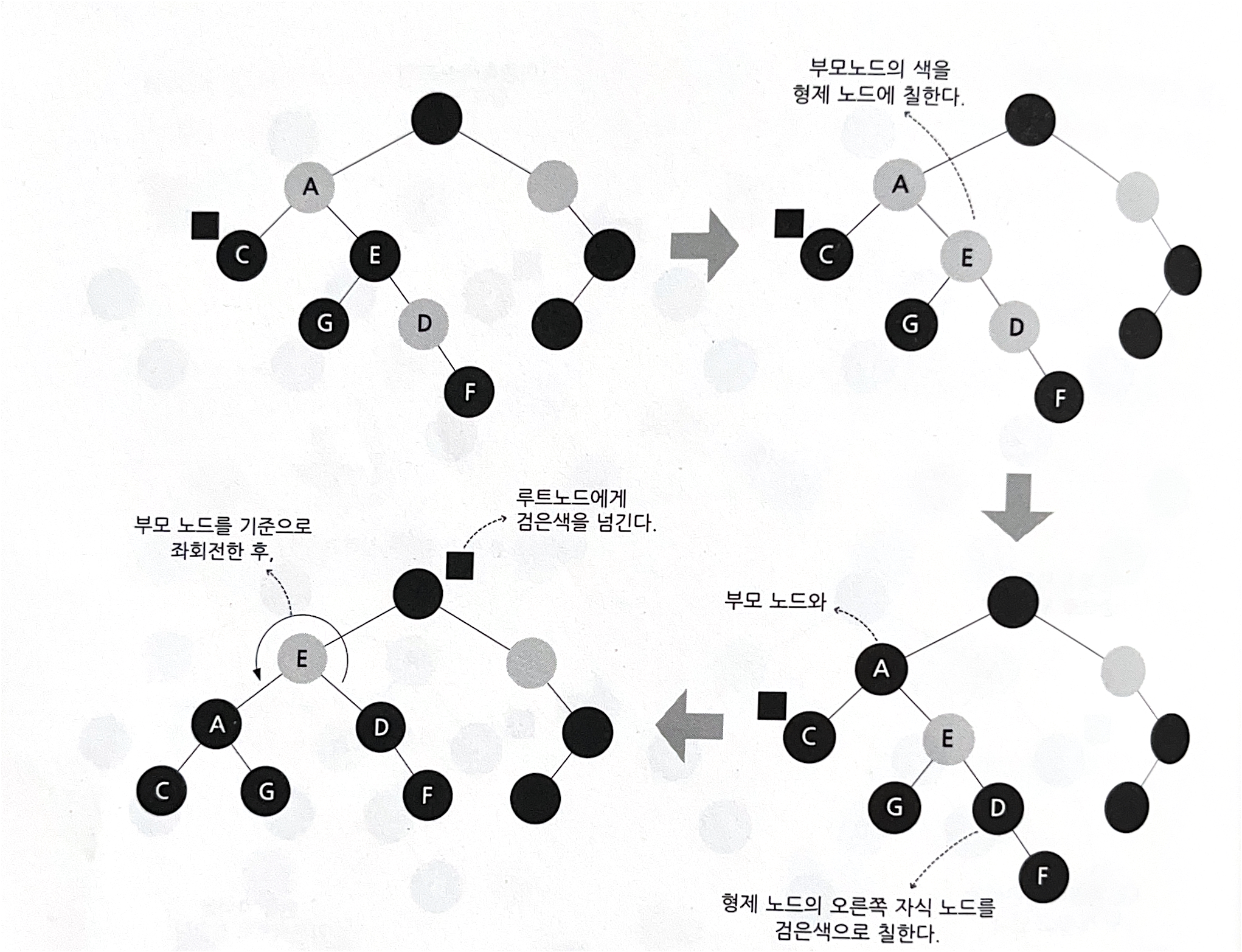
=>이중 흑색 노드의 부모노드가 가진 색을 형제노드에 칠한다 .
부모노드와 형제노드의 오른쪽 자식을 검정색으로 칠하고 부모노드 기준으로 좌회전한다 .
마지막으로 이중흑색노드의 검정색을 루트에 넘긴다 . 이때 , 루트는 그저 검정색일뿐이다 .
이렇게 1번 문제가 해결된다 .
[코드로 구현 - 무너진 규칙의 복구]
해당 함수는 노드를 삭제하고 , 삭제한 노드가 검은색일떄 호출된다 .
//이중 흑색 노드를 Successor로 표현한다
void RBT_RebuildAfterRemove(RBTNode** Root , RBYNode* Successor)
{
//형제
BRTNode* Sibling = NULL;
//루트노드거나 빨간 노드에 이중흑색이 넘어가면 종료
while ( Successor -> Parent != NULL&&Successor ->Color == Black )
{
//이중흑색노드가 부모의 왼쪽노드일때
if(Successor == Successor->Parent->Left)
{
//형제는 부모의 우측노드
Sibling = Successor->Parent->Right
//형제의 색이 빨간색이라면
if ( Sibling->Color ==Red)
{
//형제노드의 색을 검정색으로 칠한다 .
Sibling->Color = Black;
//부모를 빨간색으로 칠한다 .
Successor->Parent->Color=Red;
//부모기준 좌회전
RBT_RotsteLeft( Root , Successor -> Parent);
// =>이제 문제는 형제의 색이 검정색인 문제일때로 바뀐다 .
}
//형제의 색이 검정색이라면
else
{
//형제의 자식 모두 검정색이라면
if(Sibling->Left->Color==Black &&
Sibling->Right->Color==Black)
{
//형제의 색을 빨간색으로 칠한다
Sibling->Color = Red;
//흑색노드를 부모에게 넘긴다 :: 부모가 빨강이면 상황 종료
Successor = Successor->Parent;
}
else
{
//형제의 왼쪽 자식이 빨간색일경우
if( Sibling->Left->Color == Red )
{
//왼쪽 자식을 검정색으로 칠한다
SIbling->Left->Color=Black;
//형제를 빨간색으로 칠한다
Sibling->Color=Red;
//형제를 우회전
RBT_RotateRight ( Root , Sibling );
//우회전을 바뀐 형제를 다시 찾아준다
Sibling = Successor->Parent->Right;
}
//오른쪽 자식이 빨간색일때 + 형제를 부모의 색으로 칠한다
Sibling->Color = Successor->Parent->Color;
//부모를 검정색으로 칠한다
Successor->Parent->Color = Black;
//형제노드의 오른쪽 자식을 검은색으로 칠한다
Sibling->Right->Cokor = Black;
//부모를 기준으로 좌회전한다
RBT_RotateLeft(Root,Successor->Parent);
//루트노드에 이중흑색을 넘긴다
Successir = (*Root);
}
}
}
}
//이중흑색을 검정색으로
Successor->Color=Black;
}[코드로 구현 - 삭제 ]
위의 RBT_RebuildAfterRemove는 노드를 삭제한후, 삭제한 노드가 검은색일떄 호출된다 .
다음의 삭제 함수는 이진탐색트리와 같이 재귀호출을 사용하지 않는다 .
노드의 찾음은 RBT_SearchNode에 위임하고 , RBT_SearchNode가 찾아낸 노드는 부모노드가 있기애
부모노드의 포인터를 매개변수로 받지 않음도 다르다 .
결국, 중요한 차이는 레드블랙트리의 무너진 규칙을 복원하는 RBT_RebuildAfterRemove를 호출하는 점이다 .
RBTNode* RBT_RemoveNode (RBTNode** Root,ElementType Data)
{
RBTNode* Removed = NULL;
//대체 노드
RBTNode* Successor = NULL;
RBTNode* Target = RBT_SearchNode((*Root),Data);
if(Target==NULL)
return NULL;
//자식이 한쪽만 있는 경우 (혹은 자식이 없거나)
if(Target->Left == NIL || Target->Right == NIL)
{
Removed = Target;
}
//자식이 양쪽 다 있는경우
else
{
//오른쪽 자식의 최소값 노드를 찾아 제거,현재의 노드 위치에 둘것임
Removed = RBT_SearchMinNode( Target->Rigjt);
Target->Data = Removed->Data;
}
//삭제노드에 왼쪽자식이 있다면
if(Removed->Left!=Nil)
//왼쪽 자식을 대체노드로
Successor = Removed->Left;
//삭제노드에 오른쪽 혹은 둘다 자식이 있다면
else
///오른쪽 자식을 대체노드로 (왼쪽노드보다 오른쪽 노드가 크기에 균형에 유리해서 그런듯?)
Successor = Removed->Right;
//대체노드와 부모노드를 연결한다 .
Successor->Parent = Removed->Parent;
//삭제노드가 루트노드였다면
if(Removed->Parent == NULL)
(*Root) = Successor;
else
{
//삭제노드가 왼쪽 자식이었다면 대체노드를 왼쪽에 연결
if(Removed == Removed->Parent->Left;
Removed->Parent->Left = Successor;
//삭제노드가 오른쪽 자식이었다면 대체노드를 왼쪽에 연결
else
Removed->Parent->Right = Successor;
}
//만약 삭제노드의 색이 검정이라면
if(Removed->Color == Black)
//레드블랙트리의 규칙을 재정립한다 .
RBT_ReBuildAfterRemove( Root,Successor);
return Removed;
}
'자료구조' 카테고리의 다른 글
| [자료구조] 우선순위 큐와 힙 - 01 . 우선순위 큐와 힙 (0) | 2023.03.30 |
|---|---|
| [ 자료구조 ] 탐색 - 04 - 3 . 레드 블랙 트리 <구현> (1) | 2023.03.12 |
| [ 자료구조 ] 탐색 - 04 - 1 . 레드 블랙 트리 <회전 , 삽입> (0) | 2023.03.07 |
| [ 자료구조 ] 탐색 - 03 . 이진 탐색 트리 (0) | 2023.03.07 |
| [ 자료구조 ] 탐색 - 02 . 이진탐색 (0) | 2023.03.03 |


